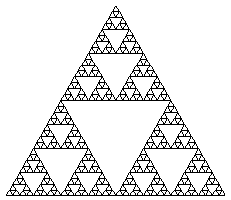Frattali, Musica, Arte e Natura
Geometria e logica frattale nella Natura, nell’Arte e nella Musica
Compilazione e impaginazione di Alan Perz
Ringraziamo Federico Miorelli, Tommaso Terragni e Vittorio Gariboldi
per le preziose informazioni e immagini fornite dal loro sito: www.miorelli.net/frattali
“Why is geometry often described as “cold” and “dry”? One reason lies in its inability to describe the shape of a cloud, a mountain, a coastiline, or a tree. Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.”
(Perché la geometria spesso viene descritta come “fredda” e “arida”? Una ragione sta nella sua incapacità di descrivere la forma di una nuvola, di una montagna, di una linea costiera, o di un albero. Le nuvole non sono sfere, le montagne non sono coni, le coste non sono cerchi, e la corteccia non è liscia, né la traiettoria di un fulmine è una linea retta.)
(Benoit B. Mandelbrot)
Così Mandelbrot nel suo libro The Fractal Geometry of Nature descrive l’inadeguatezza della geometria euclidea nella descrizione nella natura.
Mandelbrot è il padre fondatore della teoria dei frattali e inventore del famoso insieme che porta il suo nome.
Cos’è un frattale?
di Tommaso Terragni
La definizione più semplice e intuitiva lo descrive come una figura geometrica in cui un motivo identico si ripete su scala continuamente ridotta. Questo significa che ingrandendo la figura si otterranno forme ricorrenti e ad ogni ingrandimento essa rivelerà nuovi dettagli. Contrariamente a qualsiasi altra figura geometrica un frattale invece di perdere dettaglio quando è ingrandito, si arricchisce di nuovi particolari.
Triangolo di Sierpinski, 4 iterazioni
Triangolo di Sierpinski, 5 iterazioni
Il termine frattale fu coniato da Mandelbrot e ha origine nel termine latino
fractus, poichè la dimensione di un frattale non è intera, come spiegato nella sezione <
Matematica>.
Introduzione
di Tommaso Terragni
Dalla fine del XIX secolo la scienza si è orientata verso lo studio di sistemi complessi: basti pensare allo sviluppo eccezionale che ha avuto la teoria quantomeccanica o quella della relatività. Queste due teorie sono indice di come la ricerca, anche grazie a metodi matematici potentissimi e a livelli di astrazione mai raggiunti fino al XX secolo, non sia più legata all’immediata comprensibilità da parte dell’Uomo; la quantomeccanica è rappresentata da un’equazione complessa y che ha significato fisico solo se moltiplicata per il suo coniugato. L’ultima frontiera della fisica, per quanto riguarda l’unificazione delle forze, sta cercando di provare che materia, energia, spazio e tempo siano generati da vibrazioni delle supercorde, cioè oggetti indivisibili a 10 dimensioni.
Questo scenario può sembrare inquietante ed in effetti ci troviamo in una situazione simile a quella che sconvolse i filosofi e li costrinse a rinnegare Newton quando egli tentò di abbandonare la metafisica, rinunciando a definire la forza gravitazionale, ma esprimendo solo i suoi effetti: egli disse “Hypotesis non fingo”, cioè, traducendo un po’ liberamente, “non sono in grado di dirvi che cos’è la forza di gravità”, ma posso dirvi come funziona, quali sono i suoi effetti, e posso darvi degli strumenti per prevederli. L’atteggiamento del fisico moderno è sempre lo stesso, egli infatti non è interessato all’intima essenza delle supercorde ma vuole da esse derivare una conoscenza unitaria della fisica. Grazie alla teoria relativistica abbiamo molte più informazioni sull’Universo di quante potessimo ricavare dalla fisica classica.
Nonostante i grandiosi progressi fatti, oggi, scoprire le leggi fondamentali e comprendere “in principio” la struttura del mondo, non è più sufficiente. Sempre più importante diventa investigare le molteplici forme attraverso le quali si manifestano tali principi. Bisogna stare attenti a non confondere la causa con l’effetto: non è la natura che si deve adeguare alle leggi create dall’uomo per prevedere i probabili eventi; sono invece le leggi che devono diventare sempre più accurate nella descrizione di ogni tipo di fenomeno. Newton ha creato un Universo parallelo a quello reale, un universo nel quale un corpo con una certa velocità iniziale, sul quale non agiscano forze, la mantiene fino alla fine del tempo (anche esso infinito). Nulla di tutto ciò corrisponde alla realtà. Ogni corpo cambierà velocità e il tempo stesso ha avuto un inizio (e forse avrà anche una fine, se la materia dell’Universo dovesse superare un limite critico). In questo universo reale sono presenti infiniti elementi “perturbatori”, il che lo rende fondamentalmente diverso dall’universo newtoniano. Basti pensare al problema della determinazione del moto di tre corpi fra i quali vi siano forze di tipo gravitazionale, di formulazione semplicissima, eppure irrisolvibile: le equazioni che lo caratterizzano, tecnicamente, non sono integrabili (possono solo essere risolte con il metodo delle successive approssimazioni di Newton, che genera esso stesso un frattale), e quindi un minimo errore nella determinazione delle condizioni iniziali, può, alla lunga, determinare un errore non trascurabile: è quindi necessario aggiungere dati sperimentali dopo un intervallo di tempo, per limitare le imprecisioni.
Questa tendenza alla complessità, può essere bene esemplificata appunto dai frattali, figure geometriche complesse e caotiche determinate per approssimazione di una funzione ricorsiva: noi non potremo mai sapere come sia la figura finale che ha le proprietà di una frattale, ma dovremo sempre limitarci ad un’approssimazione, che può essere indicativa ma non è il frattale. È la stesso problema che si verifica nei sistemi cosiddetti “non lineari“: non è possibile determinare la situazione finale date solo le condizioni di partenza, ma bisogna continuamente aggiungere dati “sperimentali”. Queste problematiche hanno dato l’avvio allo studio del “caos deterministico“, cioè di situazioni di disordine ottenute però da processi matematico-fisici deterministici. Gli studi a proposito sono ancora in grande sviluppo e i frattali si inseriscono prepotentemente in questa nuova branca della matematica. Noi non possiamo sapere come sarà la configurazione finale del sistema a infinite iterazioni, ma sapremmo benissimo come calcolarla; è una situazione simile a quella del fisico classico che conosce perfettamente come si muove un corpo, anche considerando attriti, campi elettromagnetici dell’ambiente e del corpo stesso e tutti gli altri possibili elementi perturbatori, ma non sa il vero valore di p. Probabilmente i suoi calcoli saranno accurati a sufficienza per ogni tipo di applicazione pratica possibile e immaginabile, ma non potrebbe prevedere deterministicamente la situazione del sistema dopo un tempo infinito.
Tuttavia con lo sviluppo continuo ed esponenziale della capacità di calcolo, si possono creare figure che hanno la stessa valenza matematica per la rappresentazione del frattale vero e proprio (quello che ha, cioè, significato matematico e che gode di alcune proprietà) della valenza di un segno su un foglio per la rappresentazione della retta. Il computer si sostituisce quindi alla matita, non alla mente del matematico, che è l’unico mezzo in grado di fare della matematica. Infatti i frattali erano già stati studiati per le loro proprietà topologiche da Julia negli anni ’20, ma non erano mai stati visualizzati graficamente, né si sapeva come potesse essere la forma dei “bacini di attrazione” di una funzione che veniva continuamente iterata con se stessa. Tutto quello che è mancato a Julia è stata la capacità di calcolo che ha invece avuto B. B. Mandelbrot negli anni ’80 al centro “T. J. Watson” dell’IBM. E certamente questo, cioè riuscire a visualizzare questi strani oggetti matematici e associarli a forme presenti in Natura, ha determinato il successo di Mandelbrot; questa associazione sembra quasi svelare un progetto segreto che un’entità superiore abbia realizzato per via matematica creando la Natura. Per questo negli anni ’80 (“The fractal geometry of Nature” è del 1982) si è cercato di trovare in tutto un frattale. Si è sviluppata quindi una branca della geometria frattale che studia i cosiddetti frattali biomorfi, cioè simili ad oggetti presenti in natura. I risultati a volte sono stati stupefacenti, infatti uno dei frattali biomorfi più riusciti è la foglia di felce i cui dettagli, detti autosimili, riproducono sempre la stessa figura.
Tuttavia, per esempio, in un albero, la foglia è strutturalmente diversa dal tronco e dai rami quindi i frattali possono essere usati come analogie. Ci si potrebbe chiedere se tutto ciò sia scientificamente valido, e, considerando gli sviluppi nella direzione della complessità, io direi di sì, perché ormai le ultime frontiere della scienza non sono più comprensibili, ma vanno espresse attraverso “metafore” e “analogie”; la Scienza ha ormai bisogno di un nuovo linguaggio, adatto a esprimere l’incomprensibile per la mente umana. Non viviamo più nell’ universo liscio di Newton, ma nell’Universo delle iperconnessioni, della pluridimensionalità e della relatività, che lo rendono piegato e rugoso come un straccio. Forse non è facile accettare una situazione come questa dopo tre secoli nei quali l’universo ci è parso liscio e sicuro, illuminato dalla rassicurante presenza di Isaac Newton.
“If I have seen further than others, it is by standing upon the shoulders of giants.”
(Se ho visto più lontano di altri, è perché stavo sulle spalle di giganti.)
(Sir Isaac Newton)
Audio Albums specifici:
Album dedicato alla Musica Frattale prodotta da geometrie soniche frattali con oltre 60 minuti di musica.