Matematica dei frattali
I frattali sono figure geometriche caratterizzate dal ripetersi sino all’infinito di uno stesso motivo su scala sempre più ridotta. Questa è la “definizione” più intuitiva che si possa dare di figure che in natura si presentano con una frequenza impressionante, ma che non hanno ancora una definizione matematica precisa: l’atteggiamento corrente è quello di considerare frattale un insieme F che abbia proprietà simili alle quattro elencate qui di seguito:
1) Autosimilarità: F è unione di un numero di parti che , ingrandite di un certo fattore, riproducono tutto F; in altri termini F è unione di copie di se stesso a scale differenti.
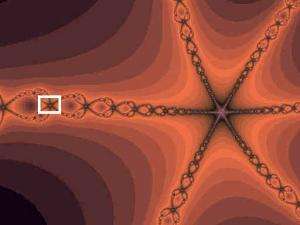
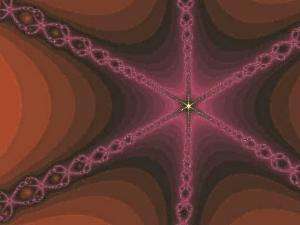
2) Struttura fine: F rivela dettagli ad ogni ingrandimento.

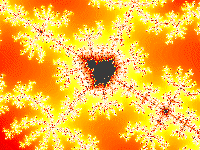


3) Irregolarità: F non si può descrivere come luogo di punti che soddisfano semplici condizioni geometriche o analitiche. (la funzione e ricorsiva: F={Z | Z = f(f(f(…)))}
4) Dimensioni di autosimilarità > della dimensione topologica
La caratteristica di queste figure, caratteristica dalla quale deriva il loro nome, è che, sebbene esse possano essere rappresentate (se non si pretende di rappresentare infinite iterazioni, cioè trasformazioni per le quali si conserva il particolare motivo geometrico) in uno spazio convenzionale a due o tre dimensioni, la loro dimensione non è intera. In effetti la lunghezza di un frattale “piano” non può essere misurata definitamente, ma dipende strettamente dal numero di iterazioni al quale si sottopone la figura iniziale.
Fino agli inizi di questo secolo la geometria ha considerato oggetti per la cui trattazione è sufficiente la definizione classica e intuitiva di dimensione (Dt=dimensione topologica), già presente almeno implicitamente in Euclide. In questa definizione, data compiutamente da Poincaré, si assegna ad un punto o a un insieme totalmente sconnesso di punti Dt=0; per le rette, induttivamente, la Dt=1 in quanto possono essere divise da elementi di Dt=0 (o meglio, un insieme F ha dimensione 1 se ogni punto ha un intorno in F arbitrariamente piccolo con frontiera di dimensione zero); e in generale un oggetto si dice di dimensione Dt=Dt’ quando ogni punto dell’insieme ha un intorno in F con frontiera di dimensione Dt=(Dt’-1). La dimensione topologica è un numero intero.
Il concetto di dimensione ha però diverse connotazioni matematiche, in accordo con le seguenti proprietà:
Siano A e B insiemi di punti:

A può essere diviso da una sottoclasse di punti Dt=(Dt’-1).
Per l’insieme di Cantor, si ha Dt(C)=0. Tale definizione non distingue tra C e l’insieme dei razionali nell’intervallo [0,1]. Per questo B. B. Mandelbrot, autorevole matematico che ha dato l’impulso allo studio dei frattali, evidenziò come la dimensione topologica non sia opportuna per le figure frattali, e per questo nello studiare queste figure si fa riferimento alla definizione di dimensione data da Kolmogorov-Hausdorff.
Si misuri un insieme di punti A con un’unità di misura h ogni volta più piccola e si chiami N(h) il minimo numero di segmenti (se il frattale è costituito da punti appartenenti ad una stessa retta) – o in generale di figure a k dimensioni se il frattale è costituito da punti tutti appartenenti ad uno spazio Âk – necessari per coprire per intero la figura, si definisce capacità di A:
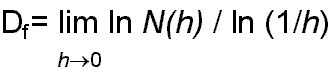
Analizziamo ora la dimensione del frattale più classico e studiato: l’insieme C di Cantor.
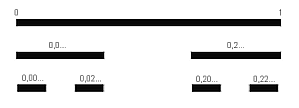
Questo insieme è costituito dai punti che “rimangono” sul segmento [0;1] dopo che da questa è stato asportato (prima iterazione, p=1) il terzo centrale (1/3; 2/3), e da ognuno dei due segmenti risultanti [0;1/3] e [2/3;1] è stato asportato il terzo centrale, esclusi gli estremi, e così via per infinite iterazioni.
Evidentemente per p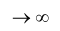 l’insieme C è costituito dagli estremi dei segmenti che si formano ad ogni iterazione, quindi è costituito da infiniti punti. La lunghezza dei segmenti asportati, dopo la p-esima iterazione, è data dall’espressione
l’insieme C è costituito dagli estremi dei segmenti che si formano ad ogni iterazione, quindi è costituito da infiniti punti. La lunghezza dei segmenti asportati, dopo la p-esima iterazione, è data dall’espressione
 l’insieme C è costituito dagli estremi dei segmenti che si formano ad ogni iterazione, quindi è costituito da infiniti punti. La lunghezza dei segmenti asportati, dopo la p-esima iterazione, è data dall’espressione
l’insieme C è costituito dagli estremi dei segmenti che si formano ad ogni iterazione, quindi è costituito da infiniti punti. La lunghezza dei segmenti asportati, dopo la p-esima iterazione, è data dall’espressione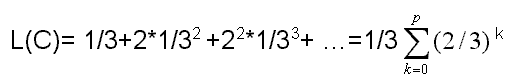
che è ovviamente uguale a 1 per p .
.
 .
.Si dimostra così che la lunghezza complessiva dell’insieme di Cantor è zero, e altresì che è costituito da infiniti punti. Quindi la definizione classica di dimensione è assolutamente inefficace. Nel 1941, cioè prima che fosse data la definizione di Kolmogorov (1958), Courant e Robbins, forse non abituati né pronti all’idea di dimensione non intera, scrissero che la dimensione di C era zero; evidentemente essi calcolarono solo la Dt, senza rendersi conto che questa è un dato sterile, che non permette di operare con questi insoliti oggetti matematici.
Oggi calcoliamo invece Df(C) prendendo inizialmente un segmento unitario, che, essendo della stessa lunghezza del segmento di partenza, lo copre al meglio; dopo la p = 1, i due segmenti rimanenti sono “misurati” da N(h) = 2 segmenti di h = 1/3; in generale, dopo p iterazioni, N(h) = 2p e h = 3–p. Da questo si ricava che
Df(C) = ln 2p / ln 1/3 -p = ln 2 / ln 3 è 0,6309…
Il fatto che la dimensione di C sia 0 < Df(C) < 1, fa immediatamente capire come l’insieme C non contenga segmenti continui, ma sia costituito da infiniti punti, che sono tutti di accumulazione per C stesso, infatti in ogni intorno U(x ε C, ε) esistono infiniti punti derivanti dalle iterazioni successive, e quindi C è un insieme perfetto perché non ci sono punti di accumulazione di C che non appartengano a C stesso (tutti gli estremi dei segmenti appartengono a C).
E’ interessante osservare che questi infiniti punti hanno la potenza del continuo! Infatti a ogni numero x ε[0, 1], si può associare la rappresentazione ternaria della misura della distanza dallo zero, e si può scrivere nella forma: x = 0,a1a2…an, dove ai = 0 oppure 1 oppure 2. Tale rappresentazione non è unica: per esempio 1/3 = 0,1(0) ma anche 1/3 = 0,0(2); in simili casi decidiamo di scegliere la rappresentazione che contiene meno cifre “1”; in tal modo, ogni numero è rappresentato in modo univoco. Si può dimostrare che x appartiene all’insieme di Cantor se e solo se la sua rappresentazione (in base 3) non contiene la cifra 1.
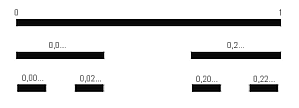
Si osservi ora che le rappresentazioni composte con le cifre 0 e 2 sono tante quante quelle composte con le cifre 0 e 1 e di queste ultime ve ne è una infinità continua (cioè con la potenza del continuo), poichè ogni numero dell’intervallo [0;1] si può rappresentare con una tale successione usando il sistema binario. In conclusione i punti di Cantor sono un’infinità continua.
Inoltre, un aspetto interessante della matematica dei frattali è l’utilizzo di una numerazione in basi diverse da quella decimale in relazione alle caratteristiche del singolo motivo geometrico. Questo procedimento è utile soprattutto per l’elaborazione da parte di computer, che non sono legati a nessuna base (diversa da quella binaria) più che a quella decimale. In questo modo, per esempio, prendendo un segmento unitario e utilizzando la base 3, l’insieme di Cantor è semplicemente costituito da tutti quei punti xn per i quali la misura della distanza d(xn) dall’estremo che noi chiameremo zero (o origine del segmento) è espressa come una successione infinita di cifre ternarie 0,a1a2…an, dove il valore delle ai sia solamente zero o due. Infatti riscontriamo che, dopo la prima iterazione, i punti del primo terzo hanno 0 ≤ d(xprimo terzo) ≤ 0,1 e che i punti del terzo di segmento adiacente al secondo estremo hanno 0,2 ≤ d(xultimo terzo) ≤ 1. Per la proprietà di autosimilarità, questo ragionamento può essere esteso alla seconda iterazione, considerando la seconda cifra dello sviluppo ternario della misura della d(x) dei punti che appartengono all’insieme dopo lap = 1. Facilmente si capisce come anche il punto x | d(x) = 0,1 appartenga all’insieme, scegliendo opportunamente la rappresentazione di 0,1 = 0,0(2).
Altri frattali vengono creati da computer attraverso l’uso di basi numeriche non decimali. Consideriamo per esempio la curva di Von Koch, nata come esempio di curva priva di tangente in alcun punto.
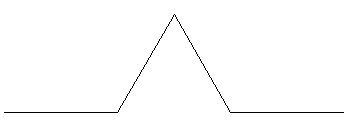 p=1
p=1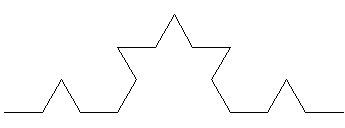 p=2
p=2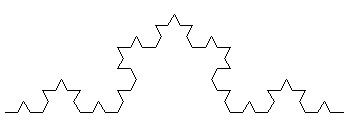 p=3
p=3Per questa curva Df(K) = ln 4 / ln 3, per p ―› ∞, mentre la sua lunghezza è evidentemente (4/3)p, cioè infinita: per disegnare perfettamente questa curva, anche supponendo di poterlo fare alla velocità della luce, sarebbe necessario un tempo infinito. Se prendiamo due punti appartenenti a K, con distanza euclideae comunque piccola, la lunghezza della curva che porta dal primo al secondo (e viceversa) è infinita. Inoltre, se costruissimo una curva di Koch su ogni lato di un triangolo equilatero, la lunghezza del perimetro della figura così ottenuta sarebbe infinita come già visto, mentre la sua area, posta l’area iniziale del triangolo Ai = a,
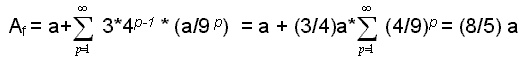
Ora abbandoniamo i frattali “semplici”, generati cioè da successive trasformazioni geometriche e consideriamo invece frattali F costituiti dai punti che soddisfano una funzione complessa R 2 (anche se, teoricamente, non c’è un limite alla dimensione topologica di un frattale, per comodità di rappresentazione noi studieremo solo frattali Julia e Mandelbrot, che si rappresentano nel piano di Argand-Gauss, facendo quindi uso della matematica complessa) del tipo Z = f(z), dove zp = Zp-1, cioè una funzione nella quale per ogni iterazione, z assume il valore di Z ottenuto nell’iterazione precedente.
In altre parole, F = { Z | Z = f(f(f(f(…)))) }
E’ proprio questo che genera l’indefinitezza che è una delle caratteristiche peculiari di tali costruzioni matematiche, ovvero la possibilità di iterare virtualmente all’infinito per ciascun punto prima di passare al successivo. Quindi, per “disegnare” un frattale attraverso un elaboratore, è necessario precisare il numero massimo di iterazioni: un tempo finito non basterebbe per calcolare un punto del frattale a infinite iterazioni.
Volendo essere un po’ più precisi, si può dire che un frattale non rappresenta altro che la “forma” del bacino di attrazione di una successione a valori complessi definita per ricorrenza, rappresentata sul piano di Argand-Gauss.
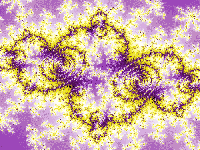
Utilizzando la funzione f(z): Z = z2 + c si ottengono i due tipi di frattali che noi studieremo principalmente: i famosi “Julia” e “Mandelbrot” (che sono generati dalla stessa equazione, ma con valori differenti per il parametro c).
L’equazione è quella che nella rappresentazione abituale genera una parabola (se z ε R) traslata col vertice in (0, c); quello che interessa a noi, tuttavia, non è la solita rappresentazione sul piano cartesiano (ovvero secondo un incremento della variabile indipendente), ma come si comporta, dato un punto di partenza, reimpostando nell’equazione i risultati dell’elaborazione precedente (zp = Zp-1).
Con l’aiuto dei calcolatori e utilizzando opportunamente i colori è possibile ottenere immagini molto suggestive di questi frattali.
Dalla determinazione delle condizioni di partenza, dipendono le differenze tra gli insiemi di Julia e l’insieme di Mandelbrot. E’ necessario un esempio, perché gran parte della difficoltà iniziale che si incontra avvicinandosi ai frattali sta in questo.
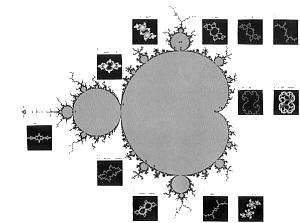
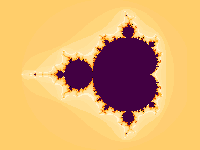
L’insieme di Mandelbrot si presenta come un otto disposto in orizzontale sfrangiato e simmetrico rispetto all’asse delle ascisse.
- Si supponga di considerare una piccola porzione attorno all’origine di un piano complesso di intervallo (-2, -2) – (2, 2).
- Si sostituiscano, per ogni punto considerato, le corrispondenti coordinate complesse al termine noto c, nell’equazione Z = z2 + c, ponendo inizialmente z = 0 + 0i.
- Si calcoli il valore di Z.
- Se si trova che la distanza di Z dall’origine è maggiore di due, si salti al passo 6. Per calcolare tale distanza, si adotta il teorema di pitagora nel seguente modo: dato Z = a + bi, il quadrato della distanza ddall’origine sarà d2 = a2 + b2.
- Se no, si incrementi di 1 un contatore e si torni al passo 3 se il contatore ha un valore inferiore al numero di iterazioni massime prefissato, dopo aver posto z = Z.
- Si colori il punto di un colore diverso a seconda del valore del contatore.
- Si azzeri il contatore e si ritorni al passo 2, per calcolare il colore del prossimo punto.
- Il procedimento avrà termine quando tutti i punti interessati saranno stati processati nel suddetto modo.
Possiamo adesso entrare un poco più in dettaglio ed affrontare i principi di determinazione dei frattali della famiglia di Julia, che si presentano molto diversamente a seconda della scelta del termine noto c.
- Si supponga considerare una piccola porzione attorno all’origine di un piano complesso di intervallo (-2, -2) – (2, 2).
- Si scelga un binomio complesso c assegnando valori del tutto arbitrari alla parte reale ad alla parte immaginaria.
- Si sostituiscano, per ogni punto considerato, le corrispondenti coordinate complesse alla variabile z, nell’equazione Z = z2 + c.
- Si calcoli il valore di Z.
- Se si trova che la distanza di Z dall’origine è maggiore di due, si salti al passo 7. Per calcolare tale distanza, si adotta il teorema di Pitagora come spiegato sopra.
- Se no, si incrementi di 1 un contatore e si torni al passo 4 se il contatore ha un valore inferiore al numero di iterazioni massime prefissato, dopo aver posto z = Z.
- Si colori il punto di un colore diverso a seconda del valore del contatore.
- Si azzeri il contatore e si ritorni al passo 3 per calcolare il colore del prossimo punto.
- Il procedimento avrà termine quando tutti i punti interessati saranno stati processati nel suddetto modo.
N. B. Il numero di iterazioni massime determina la precisione da adottare per la rappresentazione dell’insieme e per ottenere migliori risultati, è consigliabile che sia uguale o comunque inferiore al numero di colori disponibili.
Buoni risultati si ottengono assegnando a c dei coefficenti reali ed immaginari compresi fra 0 ed 1.
Vi sono infiniti insiemi di Julia poichè la scelta di c non deve sottostare a nessuna restrizione.
La differenza fra l’insieme di Mandelbrot e gli insiemi di Julia è che le coordinate complesse del punto del piano vengono sostituite non a z, inizialmente azzerato, ma a c, che non è più una costante definita all’inizio dell’elaborazione.
Questa immagine mostra l’insieme di Mandelbrot ottenuta con un numero crescente di iterazioni massime: come si può notare, la precisione del disegno dei confini diventa sempre più accurata.

