Musica coerente con intonazione a 432 Hz
Cos’è la musica con intonazione (tune) e accordatura a 432 Hertz
di Marco Amadeux Stefanelli, Ph.D.
Da un po’ di tempo a questa parte si parla molto di musica a 432 Hz (Hertz). Spesso noto però una certa confusione e alcune imprecisioni circa questo argomento, a volte addirittura una fantasia inventiva molto arbitraria e/o senza un minimo di evidenze scientifiche, perciò vedrò di chiarire ed approfondire alcuni aspetti, specialmente tecnici, riguardo a questa tecnica e definizione.
Diciamo subito che accordare e/o intonare semplicemente uno strumento a 432 Hertz non basta per raggiungere l’armonia perfetta o delle sfere. Il concetto di armonia è molto più ampio e complesso. Per raggiungere l’armonia “suprema” occorre considerare un insieme di parametri e rapporti molto complessi di vibrazioni e risonanze armoniche a vari livelli (vedi per es. il nostro progetto HRM).
Dal punto di vista psicoacustico, nella nostra analisi, dobbiamo sempre tener presente che il sistema uditivo umano si abitua inconsciamente ad un determinato diapason o accordatura. Questo è dimostrato anche da uno studio fatto nel 1994 dal professor Daniel J. Levitin, psicologo e neuroscienziato americano che dimostrò come ogni persona possieda una piccola percentuale di orecchio assoluto dovuta all’abitudine di ascoltare musica ad un determinato diapason; questa abitudine inconscia rende gli ascoltatori capaci di notare minime variazioni nell’intonazione e la sensazione che scaturisce da un rapido cambio di intonazione è la sorpresa, effetto che in molti casi può risultare sgradevole e fastidioso.
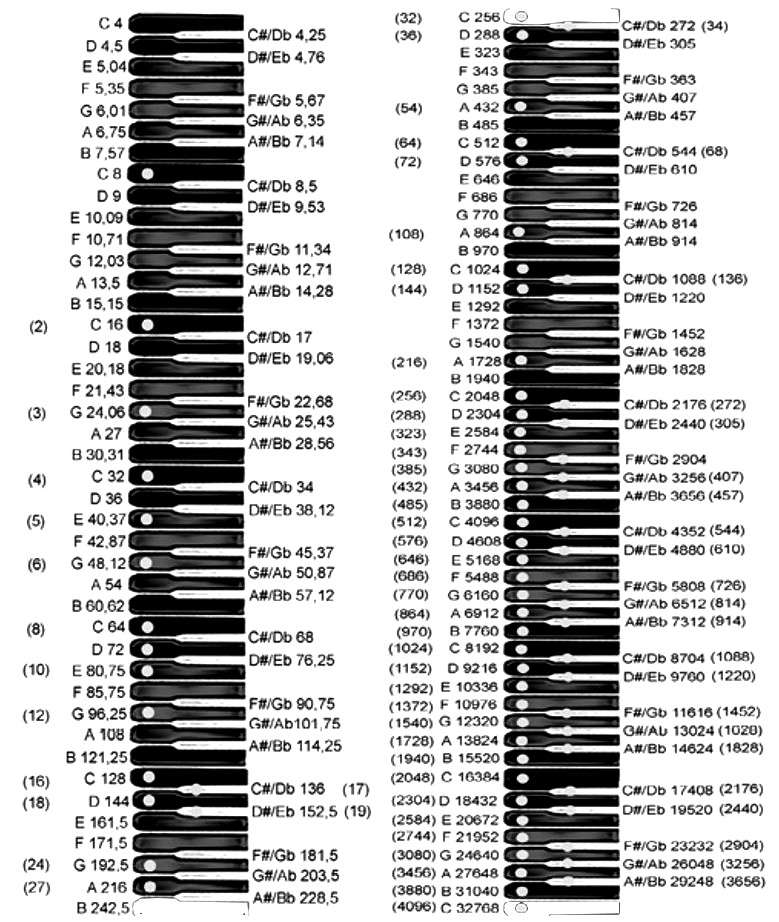
Quando si parla di musica e di note è necessario considerare innanzitutto l’intonazione e i rapporti tra le frequenze delle diverse note (accordatura) e quindi delle scale. I valori assoluti di queste frequenze probabilmente non avrebbero molta importanza se si eseguissero soltanto brani suonati da un solo strumento o cantati da una sola voce. Ma, se si devono eseguire brani a più strumenti o a più voci, bisogna partire da un punto comune, cioè accordare tutti gli strumenti a una stessa nota di riferimento che abbia una ben determinata frequenza e anche ad una stessa scala.
A questo scopo è stato scelto il LA (centrale) della terza ottava del pianoforte che nella scala naturale (diapason “naturale”) corrisponde a 432 Hertz ma che è stato fissato convenzionalmente a una frequenza di 435 Hertz dalla Accademia delle Scienze di Parigi nel 1858 e confermato dalla Conferenza internazionale di Vienna.
Giuseppe Verdi nel 1884 scrisse una lettera indirizzata alla Commissione musicale del governo italiano in cui chiese di ufficializzare l’utilizzo del corista (diapason) a 432 Hz e scrivendo al riguardo la frase: “per esigenze matematiche”, ottenne un decreto legge che normalizzava il diapason ad un LA di 432 oscillazioni al secondo. Verdi, Mozart e altri musicisti accordavano la loro orchestra a 432 Hz.
La stessa opinione di Verdi la espressero i fisici Sauver, Meerens, Savart e gli scienziati italiani Montanelli e Grassi Landi con un decreto che fu approvato all’unanimità al congresso dei musicisti del 1881 (diapason scientifico).
Nel 1939 il ministro della propaganda nazista Joseph Goebbels impose il diapason a 440 Hz contro il referendum dei 25.000 musicisti in Francia contrari a questa scelta.
La corsa all’acuto iniziò al tempo delle bande militari russe e austriache ai tempi di Wagner (con un diapason da 440 Hz a 450 Hz), e fu frutto di un’analisi delle reazioni che il suono suscita in chi lo percepisce.
Tale misura, nel 1954 a Londra, venne fissata per praticità e sempre convenzionalmente, a 440 Hertz, valore adottato dall’American Standards Association nel 1936 e a tutt’oggi dalla maggior parte dei musicisti occidentali.
Le composizioni musicali sono costituite da una successione e da una sovrapposizione di note, cioè di suoni di determinate frequenze.
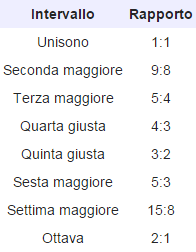
Già a Pitagora era noto che due suoni sono gradevoli all’orecchio quando il rapporto tra le loro frequenze (intervallo) è espresso mediante numeri piccoli (1:1 o 2:1 o 3:2, ecc.).
Più piccoli essi sono e migliore è l’accordo; più ci si allontana dai numeri piccoli e maggiore è la dissonanza.
Il sistema di ottimizzazione di Pitagora è basato sul rapporto. Non si basa su una intonazione assoluta, ma piuttosto sulle relazioni di intonazione di riferimento arbitrario.
I rapporti e gli intervalli tra le varie note sono stabiliti dalle scale. Esistono molti modi per definire una stessa scala. Ad esempio, le note della scala di DO si possono ricavare in diversi modi. Ne vedremo due fondamentali, la Scala Naturale e la Scala Temperata.

Scala Naturale o Cromatica (Archita/Zarlino):
La scala naturale è l’unica scala che non genera battimenti (acustici).
La scala naturale è costituita da sette note fondamentali: DO, RE MI, FA, SOL, LA, SI.
Se f è la frequenza (in Hertz) della nota fondamentale DO, le altre note hanno le frequenze:
DO f; RE 9/8 f; MI 5/4 f; FA 4/3 f; SOL 3/2f ; LA 5/3 f; SI 15/8 f; DO2 2 f.
La nota DO2 (DO della seconda ottava), che ha frequenza doppia di DO (DO della prima ottava), inizia un’altra serie di sette note che hanno tra loro rapporti di frequenze uguali a quelli delle precedenti sette note. Ciascuna serie di 7 note si chiama ottava.
L’intervallo tra le stesse note di due ottave successive (intervallo di ottava) è uguale a 2.
La scala è arricchita di note, introducendo i diesis e i bemolle tra due note successive, eccettuato tra il MI e il FA e tra il SI e il DO dell’ottava superiore.
Si dice diesis di una nota, la nota (più alta) avente con la prima l’intervallo 25/24.
Si dice bemolle di una nota, quella nota (più bassa) che ha con la prima l’intervallo 24/25.
Nella scala naturale gli intervalli tra le note non sono tutti uguali. Alcuni strumenti musicali, come il violino, permettono di produrre tutte le note della scala naturale, non così gli strumenti a tastiera.
Partendo dal SI si ottengono le note salendo di quinta in quinta (una quinta corrisponde ad un intervallo di tre toni più un semitono) trovando FA#, DO#, etc. e poi partendo da FA e scendendo di quinta in quinta e trovando SIb, MIb etc. Realizzando le scale in questo modo succede che il DO# ed il REb, ad esempio, non coincidono.
Scala Temperata (temperamento equabile):
Per semplificare le cose e per ovviare agli “inconvenienti” della scala naturale, alla fine del 1600, Andreas Werckmeister (seguito poi da J. Sebastian Bach che ne esplorò sistematicamente le potenzialità) introdusse la Scala Temperata (temperamento equabile):
Nella scala temperata gli intervalli tra due note successive sono sempre uguali. L’intervallo di ottava è diviso in 12 intervallini di un semitono ciascuno. L’ottava viene suddivisa in dodici semitoni uguali, per cui l’intervallo di un semitono è pari a:
Tra le note DO-RE, RE-MI, FA-SOL, SOL-LA, LA-SI della scala temperata vi è l’intervallo di due semitoni; tra MI-FA e SI-DO vi è l’intervallo di un solo semitono.
Tra due note aventi l’intervallo di due semitoni è intercalata una nota intermedia che corrisponde ai diesis e bemolle della scala naturale.
Se f hertz è la frequenza di DO1, risulta:
DO1 f; DO# = REþ 1.05946^1 f; RE 1.05946^2 f; RE# = MIþ 1.05946^3 f; …; DO2 1.05946^12 f.
Nella scala temperata tutti gli intervalli, e quindi le note, risultano alterati rispetto a quelli della scala naturale.
Ad esempio, se f è la frequenza di un DO, risulta:
RE naturale: 9/8 f = 1.125 f
RE temperato: 1.05946^2 f = 1.122 f.
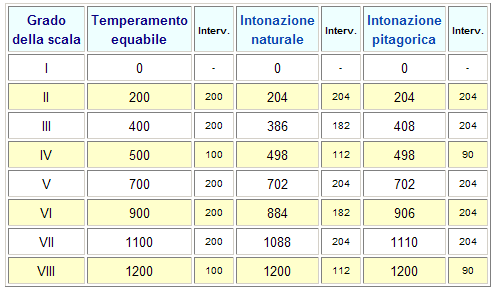
Tabella delle altezze (in cent) dei gradi della scala maggiore secondo i vari metodi di intonazione.
Come si vede, in tutti e tre i metodi l’intervallo di ottava è identico (1200 cents) e sono praticamente uguali anche gli intervalli di quarta (498-500 cents) e di quinta (700-702 cents). Il discorso è ben diverso per gli intervalli di terza maggiore e di sesta maggiore. L’intervallo di terza maggiore naturale vale 386 cents, mentre quello pitagorico è assai crescente: 408 cents; un discorso analogo vale per la sesta. Si può dunque ben capire come mai un intervallo perfettamente consonante secondo la nostra sensibilità come quello di terza maggiore venisse considerato intollerabilmente dissonante agli inizi della polifonia, quando si usava il temperamento pitagorico: la “colpa” era insita nella costruzione pitagorica della scala.
La tabella mostra anche che le approssimazioni introdotte con il temperamento equabile sono più modeste di quelle pitagoriche (l’intervallo di terza maggiore vale 400 cents invece dei 386 cents naturali) e tali da essere ormai ampiamente tollerate. Ciò spiega come mai al nostro orecchio intervalli di terza suonino consonanti anche quando suonati al pianoforte (che è intonato secondo il temperamento equabile).
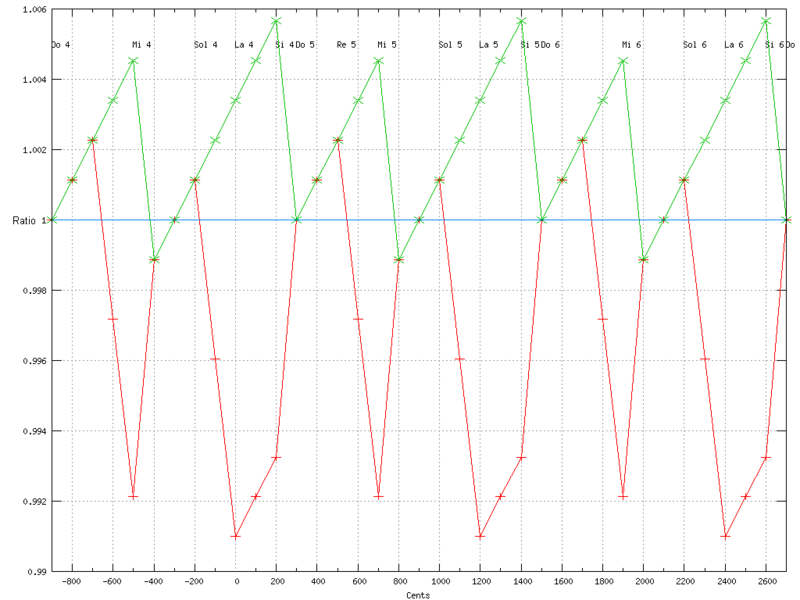
Deviazione relativa dal temperamento equabile.
Verde: temperamento pitagorico, Rosso: temperamento naturale.
Verde: temperamento pitagorico, Rosso: temperamento naturale.
Come possiamo notare, quindi, quando si parla di musica a 432 Hertz si definisce quasi esclusivamente la frequenza d’intonazione del LA centrale, ma sarebbe opportuno definire anche la scala adottata perché dal punto di vista psicoacustico e musicoterapeutico è importante sia il rapporto tra le frequenze delle note che la semplice accordatura dell’intonazione.
Intervalli e Musica
In musica si dice intervallo la distanza tra due note o suoni, cioè la differenza d’altezza tra due suoni, esprimibile in fisica acustica tramite il rapporto delle loro frequenze.
A causa della fisiologia di percezione del suono, l’intervallo musicale non è proporzionale alla differenza tra le frequenze dei suoni, ma alla differenza tra i loro logaritmi, cioè al rapporto tra le frequenze, una sorta di distanza numerica tra due suoni che si può verificare tra due suoni prodotti consecutivamente, e in tal caso si parlerà di intervallo melodico o diacronico o salto, oppure tra due suoni prodotti simultaneamente, e si dirà intervallo armonico o sincronico o bicordo.

Nella teoria musicale, gli intervalli si misurano contando le note da quella di partenza a quella di arrivo.
Se si hanno ad esempio un DO e un SOL, l’intervallo è una quinta perché si contano cinque note – DO, RE, MI, FA e SOL. L’intervallo tra il DO e sé stesso non si chiama “di prima”, ma unisono.
Si possono poi avere intervalli anche oltre l’ottava: nona, decima, undicesima e tredicesima sono quelli che si trovano menzionati più spesso.
La classificazione degli intervalli musicali costituisce argomento fondamentale nello studio della musica e del suo linguaggio. Un intervallo viene detto armonico quando i suoni che lo formano sono contemporanei e melodico se i suoni che lo formano vengono considerati in successione.
L’intervallo armonico viene sempre considerato ascendente, cioè dal grave verso l’acuto (dal basso verso l’alto). Un intervallo armonico è caratterizzato anche da consonanza e dissonanza, fenomeni legati all’interferenza generata dai due suoni in questione.
Quello melodico invece, a seconda di come è scritto, può essere ascendente o discendente, a seconda che la prima nota sia più grave dell’altra o viceversa. In pratica se ne osserva l’evoluzione in senso temporale. Un intervallo melodico si distingue anche per la direzione, ascendente o discendente, a seconda che il secondo suono sia rispettivamente più acuto o più grave rispetto al primo.
Un intervallo è detto semplice quando sta nell’estensione di un’ottava; se invece ne oltrepassa i limiti si dice composto. Va però detto che alcuni trattati di teoria considerano semplice anche l’intervallo di nona.
L’intervallo più semplice da generare è probabilmente quello di ottava. Esso si ottiene ad esempio sollecitando una corda elastica per produrre la nota più grave, dimezzando quindi la lunghezza della corda e sollecitandola nuovamente per generare la nota più acuta.
Il più piccolo intervallo utilizzato nella musica occidentale è detto semitono. Per motivi storici nel nostro sistema musicale si è scelto convenzionalmente di suddividere l’ottava in 12 semitoni equalizzati, ossia per i quali si mantenga costante il rapporto tra le frequenze degli estremi.
Nella terminologia convenzionale occidentale gli intervalli vengono classificati mediante due parametri che chiameremo ampiezza e specie. Nonostante che tutti i trattati di Teoria e di Armonia concordino nel classificare gli intervalli mediante due parametri, è curioso che in letteratura non esista in proposito una terminologia universalmente accettata. All’occorrenza vengono adottati vocaboli quali denominazione, specie, forma.
Quindi la denominazione degli intervalli si compone di due parti distinte, come ad esempio: quinta giusta, settima eccedente e così via.
Si osservi che la classicazione risulterà del tutto indipendente dalla tonalità in cui l’intervallo si presenta, infatti la definizione univoca di un intervallo dipende esclusivamente dal nome delle note che lo compongono e dal loro stato di alterazione.
Nell’armonia classica o tonale, che poi è quella che viene anche usata per descrivere canzonette, jazz e blues, si suppone che ogni brano possegga una sua tonalità di base (generalmente è l’accordo che termina il ritornello) e tutti gli accordi del pezzo vengono considerati non in assoluto, ma relativamente a quella tonalità.
È vero che si può cambiare tonalità all’interno di una canzone: ad esempio, dopo un giro di DO (DO, LAm, REm, SOL7, DO) si può avere un LA7 e rifare la stessa melodia un tono sopra, ma in questo caso si comincia semplicemente a calcolare tutti gli accordi relativamente alla nuova tonalità.
Si è deciso poi di chiamare gli intervalli relativi alla tonalità di partenza in ben due modi diversi. Il primo è il grado, e non è molto diverso dall’intervallo in sé: la nota della tonalità stessa (il DO, se siamo in DO maggiore) è il primo grado, quella che forma un intervallo di seconda con essa (in questo caso il RE) è il secondo grado, e così via fino al settimo grado.
Ma è anche possibile chiamare le note “per nome”. Il primo grado è la tonica, perché dà appunto la tonalità; il secondo grado è la sopratonica.
Passiamo poi alla modale, detta così perché definisce il modo (maggiore o minore) della tonalità, e che sta sul terzo grado. Il quinto grado è la dominante, perché nell’armonia classica è quello più importante subito dopo la tonica; quarto e sesto grado sono rispettivamente sottodominante e sopradominante, il settimo grado è la sensibile. La “settima di dominante”, se siamo in tonalità di DO, sarà la nota che fa un intervallo di settima con il SOL, che è la dominante del DO; insomma, un FA.
L’intervallo è un elemento che conferisce contenuto “oggettivo” alla musica, infatti tutte le persone che sperimentano liberamente l’intervallo vivono lo stesso contenuto e la stessa magica energia.
Tutti gli elementi fondamentali della musica possono diventare terapeutici, soprattutto gli intervalli. Ogni melodia ha in sé il contenuto degli intervalli con la quale è formata. Contenuti che spesso agiscono inconsciamente sulla persona.
Una volta compresi, gli intervalli rivelano la musica come un ritmo respiratorio dell’essere che con un continuo movimento ci connette con il Cosmo.
Quando un intervallo risuona a livello fisico il pensare ne valuta l’altezza e il nostro essere più profondo ne sente la qualità.
L’esperienza dell’intervallo, a livello cosciente, è sempre completa ed equilibrata. Tale fenomeno fa parte del ritmo respiratorio animico-spirituale che sta alla base dell’intervallo. Come in ogni inspirazione vi è inclusa l’espirazione relativa e dipendente così pure negli intervalli i due movimenti sono connessi in modo che uno sia “positivo” e l’altro “negativo”.
Un parallelo potrebbe essere quello dei colori in cui l’occhio, a livello fisiologico, percependo un colore risponde producendo il colore complementare e quindi polarmente opposto. Si genera così un costante equilibrio tra esterno e interno.
Attraverso una lunga evoluzione, l’essere umano ha forgiato i suoi strumenti, coadiuvato dagli elementi musicali, specialmente gli intervalli. Possiamo dire infatti che l’ottava degli intervalli è la “misura” dell’Uomo.

Intonazione scala Temperamento equabile basata su Accordatura DO 256 Hz / LA 432 Hz
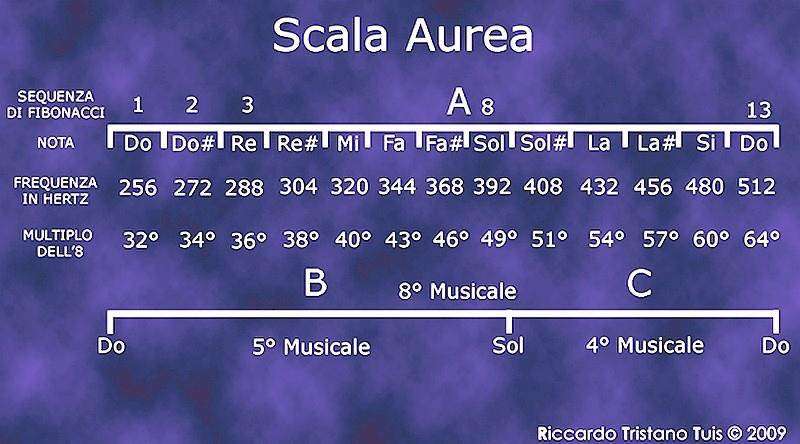
Intonazione scala Aurea di R. T. Tuis basata su Accordatura DO 256 Hz / LA 432 Hz
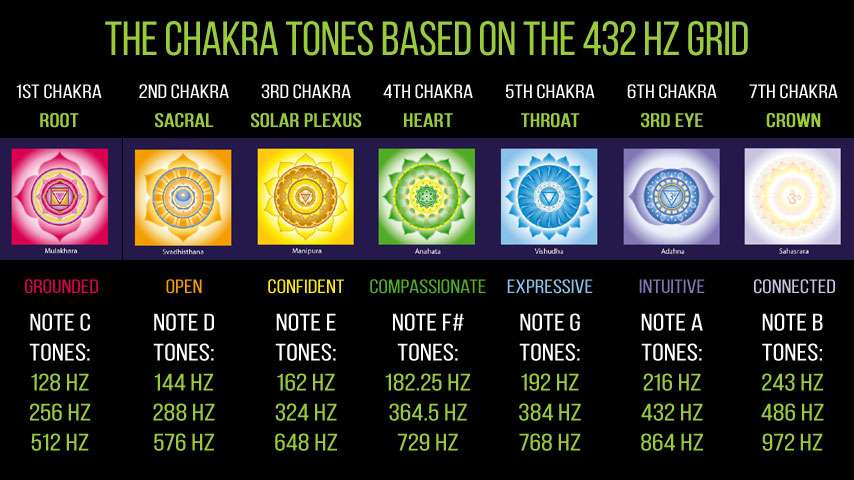
(Frequenze Temperamento Equabile basato su Intervallo 1,05946 e LA = 432 Hz)
(Tabella frequenze scala Pitagorica basata su LA = 432 Hz)
(Tabella frequenze scala Naturale basata su LA = 432 Hz)
(Frequenze scala AUMega A. Bosman basata su LA = 432 Hz)
Scala AUMega di A. Bosman basata su DO=256 Hz – LA = 432 Hz
Accordatura e intonazione Aurea scientifica
(fonte: Wikipedia)
L’accordatura aurea o scientifica si riferisce a una speciale intonazione, storicamente impiegata in alcuni teatri e corti europee, che fissa il la centrale a 432 Hz (Hertz). Con i rapporti tra le note determinati in base al temperamento equabile, il DO centrale risulta intonato a 256,87 Hz, anziché ai circa 261,62 Hz dell’intonazione standard (con il LA a 440 Hz). Se invece si utilizza l’antica scala pitagorica, il medesimo DO risulta alla frequenza di 256 Hz.
Il DO a 256 Hz è adottato anche in alcuni documenti scientifici per comodità di calcolo: la frequenza dei DO di tutte le ottave risulta una potenza di 2 (utile a fini computazionali)[1].
Secondo alcuni, la musica suonata secondo l’accordatura aurea (con il DO a 256 Hz) porterebbe benefici misurabili alla salute degli ascoltatori[2]. Molti promotori affermano che esista una relazione tra la centratura a 432 Hz e il fenomeno della risonanza di Schumann.
Tuttavia si deve considerare che, con il DO centrale a 256 Hz, un’accordatura basata sul temperamento equabile canonico porta ad avere il LA intonato a:
(non a 432 Hz), mentre solo l’uso della scala pitagorica fornisce:
Storia
Fino al XVII secolo l’intonazione degli strumenti musicali variava molto da paese a paese, a seconda dell’uso che se ne faceva e della scuola di appartenenza dei musicisti. Il LA centrale variava quindi da 370 fino 560 hertz[3].
Jonathan Tennenbaum, in A Brief History of Musical Tuning[4], considera che tra i primi riferimenti espliciti dell’intonazione con il DO centrale a 256 hertz fu fatta dal fisico Joseph Sauveur (1653-1716), considerato il padre della fisica acustica. Joseph Sauveur, contemporaneo di J.S. Bach, sviluppò un metodo tecnico per determinare l’esatta intonazione di una nota espressa in cicli per secondo. Qualche decennio dopo un suo collega, Ernst Chladni, definì in un libro sulla teoria musicale il DO a 256 hertz come un’intonazione scientifica.
Dopo la caduta di Napoleone, nel 1815, al Congresso di Vienna lo Zar Alessandro I° chiese un suono più “brillante” e tale richiesta fu supportata poi da tutte le famiglie reali d’Europa[4]. Tale istanza fu osteggiata dai musicisti classici ma la scuola romantica, guidata dal pianista Franz Liszt e dal compositore Richard Wagner sostenne l’intonazione più alta nel periodo tra il 1830 e il 1840[2].
Nel 1859, il governo francese, sotto l’influenza di una commissione di compositori sostenitori del belcanto, uniformò per legge il LA a 435 hertz, intonazione tra le più basse del periodo. In seguito, nel 1884, il governo italiano emise un decreto per la normalizzazione del diapason a 432 vibrazioni per secondo, normalizzazione richiesta da Giuseppe Verdi e altri musicisti italiani riuniti al congresso di Milano nel 1881[5][6]. In una lettera alla commissione musicale del Governo, riportata nel decreto, Verdi scrisse[7]:
« Fin da quando venne adottato in Francia il diapason normale, io consigliai venisse seguito l’esempio anche da noi; e domandai formalmente alle orchestre di diverse città d’Italia, fra le altre a quella della Scala, di abbassare il corista uniformandosi al normale francese. Se la Commissione musicale istituita dal nostro Governo crede, per esigenze matematiche, di ridurre le 435 vibrazioni del corista francese in 432, la differenza è così piccola, quasi impercettibile all’orecchio, ch’io aderisco di buon grado. Sarebbe grave, gravissimo errore adottare, come viene da Roma proposto, un diapason di 450. Io pure sono d’opinione con lei che l’abbassamento del corista non toglie nulla alla sonorità ed al brio dell’esecuzione; ma dà al contrario qualche cosa di più nobile, di più pieno e maestoso che non potrebbero dare gli strilli di un corista troppo acuto. Per parte mia vorrei che un solo corista venisse adottato in tutto il mondo musicale. La lingua musicale è universale: perché dunque la nota che ha nome LA a Parigi o a Milano dovrebbe diventare un SI bemolle a Roma? »
A parte in Italia e Francia, le oscillazioni del diapason variavano non solo da nazione a nazione ma anche da un genere musicale all’altro (musica sinfonica, di teatro, da chiesa). Il “diapason normale” cui si riferisce Verdi è quello conservato al Museo del Conservatorio nazionale di Parigi, mentre il diapason riportato nel decreto italiano ed approvato alla unanimità al congresso dei musicisti italiani del 1881, è quello proposto inizialmente dal fisico Sauveur e poi dai suoi colleghi Meerens, Savart e dagli scienziati Montanelli e Grassi Landi.
Un anno dopo il decreto promulgato dal governo italiano sul LA a 432 hertz, un congresso a Vienna decretò che non era possibile standardizzare alcuna intonazione e nei teatri europei ed statunitensi si continuò a tenere il LA a 432-435 cicli per secondo[4].
In Gran Bretagna divenne uno standard l’intonazione con il LA a 439 hz per via di una mal interpretazione della regola francese[8]. Nel 1917 l’American Federation of Musicians accettò il LA a 440 Hz come intonazione standard e nel 1920 lo fece anche il governo statunitense. Solo nel settembre 1938, la Commissione Acustica della Radio di Berlino richiese alla British Standard Association di organizzare un congresso a Londra per adottare internazionalmente l’intonazione a 440 Hz della radio tedesca[4].
Questo congresso fu tenuto poco prima della guerra, nel maggio-giugno del 1939 e giunse a un accordo per il LA a 440 Hz, molto vicino a quella usata in Gran Bretagna. Questa frequenza fu scelta probabilmente come compromesso tra gli standard precedentemente accettati e le tendenze del momento, che vedeva salire le intonazioni[8]. In Germania fu il ministro della Propaganda nazista Joseph Paul Goebbels che spinse per la standardizzazione a questa frequenza, definendola “l’intonazione ufficiale germanica” probabilmente perché già cara a Wagner e alla scuola romantica[2].
Nell’ottobre del 1953 fu organizzato un secondo congresso a Londra dall’organizzazione internazionale per la normazione con lo stesso intento di adottare internazionalmente il LA a 440 hertz. L’ISO promosse una risoluzione in questo senso perché lo standard rimaneva non rispettato e alcune orchestre tendevano a usare intonazioni più alte[8]. Molti musicisti europei si opposero invece a questa standardizzazione per una intonazione a 432-435 Hz. Il professor Robert Dussaut del conservatorio nazionale di Parigi organizzò un referendum per il quale 23.000 musicisti francesi votarono in modo schiacciante a favore del LA a 432 cicli per secondo[4].
Solamente nel 1971 l’intonazione con il La corista a 440 Hz fu riconosciuta sul piano giuridico da una delegazione nominata dal Consiglio d’Europa a cui si adeguò anche l’Italia[2].
1^ Marshall Long, Architectural acoustics, p. 81, Elsevier, 2006 ISBN 0-12-455551-9.
2^ a b c d e Riccardo Tristano Tuis, 432 Hertz: La Rivoluzione Musicale – F.A.Q., 432hertzlarivoluzionemusicale.com. URL consultato il 3 novembre 2013.
3^ Bencivelli. Da 423 fino a 567 secondo Tuis
4^ a b c d e Jonathan Tennenbaum, A Brief History of Musical Tuning, schillerinstitute.org. URL consultato il 7 novembre 2013.
5^ Bencivelli
6^ Tale decreto è ora conservato al Conservatorio Giuseppe Verdi di Milano. Tuis
7^ a b Il disegno di legge per il La di Verdi, MoviSol.org. URL consultato il 3 novembre 2013.
8^ a b c (EN) Lynn Cavanagh, A brief history of the establishment of international standard pitch a=440 hertz (PDF), wam.hr. URL consultato il 7 novembre 2013.
9^ Una nuova iniziativa per il diapason di Verdi, movisol.org. URL consultato il 4 novembre 2013.
10^ Musica: Presentato il manuale: “Canto e diapason”, in Adnkronos, 10 giugno 1996. URL consultato il 9 novembre 2013.
11^ Stone Circles Fuzz Orchestra (Il Circo De… / Bio, su ReverbNation. URL consultato il 19 settembre 2014.

Il NAUTILUS e la “MUSICA DELLE SFERE”
estratti di Lucia Bono
Il nautilus nasconde forse la chiave di ancor più affascinanti misteri: c’è chi lascia intendere che la prodigiosa conchiglia di questo mollusco sia, per così dire, un messaggio in bottiglia lasciato al genere umano dal Creatore per consentirgli di comprendere i segreti della creazione…
La conchiglia del nautilus è forse il più bell’esempio di spirale logaritmica in natura. La forma è data dal fatto che il mollusco, che occupa solo l’ultima camera, crescendo mantiene sempre le stesse proporzioni. Il Nautilus ha la sezione del guscio come una perfetta spirale logaritmica dimostrando come il rapporto aureo Phi (= 1,6180339) sia l’espressione matematica della bellezza e della eleganza della natura.
All’interno del nicchio sono presenti circa 34-36 zone divise da pareti di madreperla, chiamate setti, che aumentano di numero con l’aumentare dell’età: sono le camere che il corpo del mollusco occupa mano a mano che aumenta di dimensione. Solo l’ultimo e più esterno dei setti è occupato costantemente dalle parti molli dell’organismo.
Il sistema musicale è rappresentabile con coordinate polari e genera una spirale logaritmica. Le “note” con le relative frequenze sono rappresentabili come distanza fra centro e circonferenza.
La spirale logaritmica ha la particolarità di essere equi-angolare. Misurando le distanze fra il centro della spirale e i punti di connessione dei setti con la circonferenza esterna del guscio, si può notare che l’angolo fra un segmento e l’altro è di 21,6° e che l’ottavo segmento ha una distanza 1,618 volte il primo, per cui corrisponde al sistema musicale in sezione aurea con Phi^n/7 per n = 1, 2,…, n.
Il Nautilus è quindi uno dei migliori esempi della spirale logaritmica in sezione aurea nella natura, con la disposizione delle sue setti che corrisponde al sistema musicale Phi con sette note per intervallo Phi.
L’angolo di ogni segmento di 21,6° non è casuale. Dividendo ogni segmento in tre, si ottiene un angolo di 7,2° (21,6°/3=7,2°) che è un decimo del angolo base di 72° di un pentagono, figura geometrica che include il valore esatto della sezione aurea.
Dai multipli di 7,2° si creano gli angoli di 36°, 72° e 108° che sono alla base del triangoli in sezione aurea basati sulla geometria del pentagono. Si ottiene anche l’angolo di 144°, sempre multiplo di 7,2°. Il numero 144 = 12*12 è un numero che appartiene alla serie di Fibonacci. Inoltre, il valore 12 è giusto la metà del numero delle vibrazioni fisiche di una stringa bosonica (24). Si ottengono anche gli angoli esatti di 180° e 360°. Infine, si ottiene l’angolo di 432° (7,2° * 60 = 21,6° * 20 = 432°).
Il numero 432 in Hz è la frequenza base del sistema che genera la serie di Fibonacci e nella rappresentazione a spirale incontriamo questo numero come angolo che include gli angoli del pentagono già menzionati (12*36°=432°, 6*72°=432°, 4*108°=432° e 144°*3=432°).
E’ interessante notare che per n=16,66666 l’angolo della spirale logaritmica corrisponde esattamente al valore dell’angolo giro di 360° (16,6666*21,6°=360°) assumendo un valore del sistema musicale di 3,144775 (Phi^16,6666/7) che è precisamente Pi Greco e ricordando che la circonferenza di un angolo giro di 360° è il diametro moltiplicato per Pi Greco.
Notiamo, inoltre, che 432° / Pi Greco = 360° / Phi^2=137,5°.
Per concludere, il numero 432 è contenuto nel sistema intonato 1=432 Hz anche come angolo di base in una rappresentazione polare (spirale logaritmica) del sistema Phi^n/7, per cui assume carattere di costante universale.”
Fin qui tutto rimane nei confini della scienza; ma subito dopo Nardelli ne trae conclusioni metafisiche, affermando che “la scelta della natura ovvero del Creatore di disporre i segmenti del Nautilus nella maniera descritta è senz’altro motivata dalla sua piena corrispondenza in armonia con le frequenze onnipresenti nell’universo, per cui è possibile prendere in considerazione che il sistema Phi^n/7 equivale all’idea che si era fatto Pitagora con il suo concetto “Tutto è numero” e del concetto della “musica delle sfere” interpretando tutto l’universo come un gigantesco strumento musicale.”
Un nuovo universo musicale: la Scala Aurea φ-tonale
di Renato Ornaghi
Con la scala aurea, la matematica ha tanto a che fare. Il simbolo φ (lettera greca, letta fi) è la cosiddetta sezione aurea (il “numero” universale per antonomasia, basato sulla serie numerica di Fibonacci e alla base di innumerevoli fenomeni fisici e biologici naturali, nonchè contenuto in numerosi e celebri capolavori dell’arte e dell’architettura). φ è forse il numero irrazionale che, insieme al numero π, più ha influenzato – nei secoli – l’arte e la cultura umana. Anche la Brianza ha ospitato tantissimi artisti che con la sezione aurea hanno avuto a che fare; tra i tanti, il genio di Leonardo da Vinci e – più vicino a noi nel tempo e nello spazio – l’architetto di Meda Giuseppe Terragni.
Il simbolo φ (lettera greca, letta phi) è da intendersi come la sezione aurea (considerato il “numero” del creato per eccellenza, basato sulla serie numerica di Fibonacci e alla base di innumerevoli fenomeni fisici e naturali, nonchè utilizzato in numerosi e celebri capolavori dell’arte e dell’architettura). φ è forse il numero irrazionale che, insieme al numero π, più ha influenzato nei secoli l’arte e la cultura umana.
Chiamato anche costante di Fidia, divina proporzione o rapporto aureo, φ è come si è detto un numero irrazionale (cioè non riconducibile a un rapporto tra numeri interi). Questa è la formula matematica che determina il valore irrazionale di φ:
Sia per le sue proprietà geometriche e matematiche, sia per la sua frequente riproposizione in molteplici contesti naturali, artistici e culturali, il numero φ ha ispirato per secoli nella mente dell’uomo la conferma dell’esistenza di un rapporto tra macrocosmo e microcosmo, tra Dio e uomo, universo e natura. Numerosi filosofi ed artisti sono arrivati a vedere nelle sorprendenti proprietà del numero φ un ideale di bellezza e armonia, spingendosi a ricercarlo e a riproporlo quale canone definitivo; testimonianza ne è la storia del nome φ, che nell’arte e nella cultura ha assunto come si è visto gli appellativi di aureo o divino.
La musica non è certo rimasta immune dalla suggestione per questo affascinante numero: molti ritengono che in essa sia infatti centrale il ruolo della sezione aurea. A sostegno di questa tesi vengono ad esempio richiamate alcune particolarità strutturali di strumenti come il violino e il pianoforte. Bartók e Debussy sono solo due tra i compositori che hanno usato in musica il concetto di sezione aurea, ma se ne potrebbero menzionare molti altri, tutti operanti tra la fine del XIX secolo e il XX secolo. In questo articolo si utilizzerà dunque la sezione aurea come fonte di ispirazione musicale da un punto di vista completamente nuovo, attraverso la creazione di una nuova scala musicale: la scala φ-tonale.
Com’è costruita la scala φ-tonale
La scala musicale φ-tonale riproduce al suo interno una successione di suoni nella quale il numero della sezione aurea è la chiave generatrice fondamentale. Essa tuttavia risulta alquanto diversa dalle altre scale conosciute, siano queste tipiche della cultura occidentale oppure appartenenti a sistemi musicali estranei al nostro (come l’indiano, il cinese, il vietnamita, ecc.). Per spiegare meglio in cosa si differenzi radicalmente la scala φ-tonale dalle altre scale musicali conosciute, è opportuna una brevissima digressione sulle scale musicali (a beneficio della comprensione per chi non sia particolarmente addentro alla teoria delle scale) e su come le note musicali di queste vengono generate.
Le scale musicali “pitagorica” e “naturale”
La scala pitagorica è tra i più primitivi sistemi di scale musicali, utilizzata a lungo nella musica più antica per la costruzione dei suoni in una specifica melodia. Conosciuta in Mesopotamia fin dal IV millennio a.C., nella tradizione occidentale essa è stata attribuita a Pitagora; fu utilizzata nell’antichità in Grecia e nell’Oriente, in Cina e poi in Giappone. Questa scala musicale è basata con rigore matematico sull’intervallo di quinta (Do-Sol, rappresentato dal rapporto delle frequenze dei suoni 3/2) e di ottava (Do-Do, rapporto delle frequenze 2/1). Fu questa la scala adottata nella musica medievale: essa soddisfaceva le semplici esigenze della composizione monodica del tempo, in cui gli accordi conclusivi contenevano solamente ottave e quinte.
A partire dal XV secolo si affermò tuttavia un uso sempre più frequente degli intervalli armonici di terza e sesta, che nella scala pitagorica risultano poco consonanti. Nel XVI secolo pertanto il musicista veneziano Gioseffo Zarlino nel suo Le istitutioni harmonicae (1558) propose una scala naturale, utilizzando altri intervalli consonanti nella scala ossia (oltre alle quinte e quarte pitagoriche) le terze maggiori rappresentate dal rapporto di frequenze 5/4 e quelle minori rappresentate dal rapporto 6/5.
La scala naturale di Zarlino è una scala musicale di chiara ispirazione pitagorica e in quanto tale basata sulla successione di suoni armonici, con però alcuni perfezionamenti: essa identifica una progressione di note che collega la frequenza di una nota alla successiva attraverso un rapporto di numeri interi, come segue:
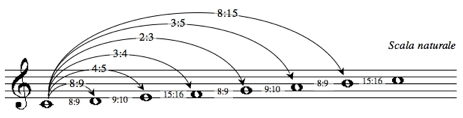
Pur essendo affascinante nella sua costruzione matematica, il problema di questa scala (che pure amplia alquanto il registro espressivo della frase musicale rispetto alla pitagorica), è che essa crea seri problemi di accordatura negli strumenti a intonazione fissa (pianoforte, chitarra, ecc.): è infatti necessario intonare nuovamente tali strumenti ad ogni cambio di tonalità. Sia per superare questo limite, sia per la necessità compositiva di poter effettuare modulazioni in diverse tonalità, i teorici musicali del XVIII secolo lavorarono nel cercare una soluzione tale da “aggiustare”, “temperare” la scala naturale, rendendo tutti gli intervalli tra i toni e i semitoni della scala equi, cioè uguali, in grado suonare omologamente in tutte le tonalità. Le soluzioni per rendere equa, “equalizzare” la scala naturale furono diverse, note in area musicale tedesca come buoni temperamenti e oggi spesso definiti temperamenti inequabili.
Il clavicembalo ben temperato di Bach (1722) fu la prima opera musicale che esplorò sistematicamente le grandissime potenzialità espressive del temperamento: a partire dal successo di quella, esso fu quindi rapidamente recepito. Ed è dunque ormai due secoli è quindi pacificamente adottata nella cultura musicale occidentale la cosiddetta scala temperata (cosiddetta a “temperamento equabile” a dodici semitoni, nella tecnica musicale nota col codice 12-tET). Tale scala consente di suddividere toni e semitoni in intervalli equidistanti e – finalmente – consente la piena modulazione nella frase musicale in tutte le dodici tonalità della scala, negli strumenti a intonazione fissa. Data l’importanza della scala temperata (che è alla base della musica classica o popolare che ascoltiamo ogni giorno alla radio), è più che mai opportuna – anche per poi comprendere la scala φ-tonale – una breve analisi della stessa.
La scala musicale temperata (12-tET)
Come si è visto, Il temperamento equabile in un sistema di costruzione della scala musicale è basato sulla suddivisione dell’ottava (cioè dell’intervallo tra due suoni aventi uno il doppio della frequenza dell’altro) in intervalli tra loro esattamente uguali. Nell’uso occidentale più diffuso (e ormai monopolizzante, tant’è che lo ritroviamo sempre negli strumenti ad accordatura fissa, in un qualsiasi negozio di strumenti musicali), l’ottava è “equamente” suddivisa in 12 parti (dette semitoni). Il temperamento così costituito, codificato come si è detto 12-tET, è il temperamento per antonomasia per il 99,99% dei musicisti occidentali.
Abbiamo già visto che questa scala è stata denominata “scala temperata” in quanto determina un leggero “aggiustamento” dei gradi della scala naturale, in modo da dare uniformità ai vari tipi d’intervallo, eliminare le ambiguità armoniche tra tono maggiore e minore e consentire la modulazione armonica tra le varie tonalità. Per questo motivo e grazie al fatto che la musica romantica e post-romantica del XIX secolo beneficiò grandemente di tale impianto formale, tra tutti i possibili temperamenti equabili il 12-tET è quello che ha preso generale diffusione, sia nella musica cosiddetta colta sia nella musica popolare.
Come si costruiscono le note della scala 12 tET? Qui occorre iniziare a introdurre un po’ più di matematica: nella scala 12 tET entrano in gioco i numeri irrazionali, in particolare la radice dodicesima del numero 2. Dato che infatti l’intervallo musicale di ottava è espresso dalla frazione 2/1 (in quanto la frequenza dei suoni raddoppia ad ogni ottava crescente e si dimezza ad ogni ottava decrescente), il rapporto di frequenze che identifica il semitono temperato nella scala di 12 semitoni è il numero irrazionale S . = 1,059463…
Fate anche voi la prova, moltiplicando 12 volte per se stesso il numero S, si ottiene il numero 2:
S x S x S x S x S x S x S x S x S x S x S x S = 2
Partendo quindi dalla nota La centrale (La3) sulla tastiera del pianoforte, che ha frequenza 440 Hz, moltiplicando 12 volte il numero 440 per il numero irrazionale S si ottengono in sequenza le 12 note della scala 12-tET, sino a giungere al La successivo un’ottava sopra (La4) a 880 Hz. Per ottenere il La# (un semitono sopra il La3), la frequenza da generare sarà dunque: 440 x 1,059463 = 466,2 Hz. E così via per tutti i dodici semitoni della scala.
In questo modo, i dodici semitoni coprono esattamente ed equanimemente l’intervallo di un’ottava, secondo questo schema:

La scala temperata 12 tET, con i suoi 12 semitoni modulabili equanimemente in tutte le dodici tonalità sulla tastiera del pianoforte, ha indubbiamente rappresentato un fondamentale punto di arrivo per la cultura musicale occidentale, dall’epoca barocco sino alla musica romantica e moderna del secolo scorso (ma anche nella musica pop, rock e jazz). Essa è di fatto al cuore della musica che oggi tutti noi conosciamo e ascoltiamo. E tuttavia ogni sistema formale artistico e culturale – come ben si sa – evolve, esige continui sviluppi. Vedremo ora quelli più recenti, per poi arrivare finalmente alla scala φ-tonale (che è poi il vero obiettivo di questa lunga – ma converrete, necessaria – digressione sulle scale musicali).
Gli sviluppi più recenti: le scale microtonali
Per microtonalità si intende l’uso di qualsiasi sistema di ripartizione dell’intervallo musicale di ottava che sia considerato “inusuale” o “diverso” per un determinato ambito culturale. in molti contesti del XX e XXI secolo, ad esempio, si parla di microtonalità per qualunque accordatura per tastiera o chitarra diversa dalla divisione dell’ottava in 12 semitoni uguali (i nostri 12 semitoni equamente temperati, ovvero l’ormai ben nota e più volte menzionata scala 12-tET).
I suoni che uno strumento microtonale appositamente progettato può generare si collocano su divisioni alternative di intervalli all’interno dell’ottava. Ad esempio, un compositore microtonale può scrivere in un sistema di scala che suddivida l’ottava in 17, 19, 22 o 31 parti uguali. La ragione che lo spinge a fare ciò è semplicemente di ricerca e di evoluzione del proprio linguaggio musicale: qualsiasi particolare divisione dell’ottava impone di fatto l’utilizzo di alcuni rapporti armonici ed impedisce l’uso di altri, esplorare le varie sfumature della tavolozza musicale è uno dei compiti e obiettivi del compositore che non vuole fermarsi.
Solo per fare un paio di esempi, la scala a diciannove semitoni 19-tET permette di utilizzare molte variazioni armoniche esotiche come quelle che si sentono nella musica mediorientale mentre la scala 31-tET ha a detta di alcuni compositori un suono particolarmente calmo e distensivo.
Ogni artista vero desidera ama conoscere al massimo il materiale di cui dispone, e soprattutto vuole andare oltre i linguaggi che già conosce. Le scale microtonali offrono questa possibilità di emigrare da regole già note (il sistema 12-tET, dopo l’esplorazione effettuata della cosiddetta musica dodecafonica, ha in sostanza esaurito le sue potenzialità espressive come sistema di segni). Una scala particolare nell’ambito microtonale è la 24-tET, che non fa altro che “spaccare il capello” del tono della scala temperata in quattro, suddividendo l’intervallo di ottava in 24 anziché 12 suoni equidistanti e giungendo alla frammentazione del semitono in due parti proporzionalmente identiche. Tutta la nostra musica occidentale – basata sui 12 semitoni della 12iET – è pertanto un “sottoinsieme proprio” della musica microtonale 24-tET. Ma è ora giunto – e finalmente, direte – il momento di parlare della scala φ-tonale.
Un’ulteriore evoluzione musicale: La scala φ-tonale
Con l’avvento della microtonalità si è passati come si è visto dalla divisione dell’ottava in 12 semitoni equidistanti a divisioni della medesima in altri multipli o sottomultipli, esplorando sistemi musicali che aprono nuovi orizzonti al compositore. Ma anche le scale microtonali (e qui sta il punto cruciale) pongono ancora un ultimo forte vincolo: tutte le possibili suddivisioni microtonali non hanno minimamente scalfito quello che è l’intervallo musicale base e più importante: l’intervallo di ottava (ovvero, quello tra due note omonime ma una avente frequenza doppia dell’altra). Un intervallo questo che, anche più complessi sistemi di scala generati dalle varie culture musicali, è rimasto sempre immune e per nulla scalfito.
Come suonerebbe mai una frase musicale, priva di questo fondamentale intervallo? Intervallo che è talmente fondamentale e fondante al punto tale che in qualsiasi sistema musicale non ci si è mai posto il dubbio di farne a meno. L’intervallo di ottava – mutatis mutandis – è dunque una sorta di Quinto Postulato della musica: in geometria pareva infatti talmente evidente ed intuitivo che da un punto esterno a una retta passasse una e una sola parallela alla retta data, che per 2000 anni di teoremi e studi geometrici non ci si è mai posti il dubbio se al Quinto Postulato potessero esistere alternative.
Eppure, perché no? Comporre senza intervallo di ottava si può fare: basta volerlo, disponendo ovviamente di una scala ad hoc. La scala φ-tonale offre appunto al compositore l’opportunità di superare questa ultima barriera musicale, un vincolo presente in ogni scala, rompendo il tabù di non utilizzare nella composizione un intervallo musicale (l’ottava) che è stato sinora ritenuto intangibile, adottando una sequenza di suoni in una scala nella quale l’ottava non risulti mai essere presente.
Creare una scala del genere non è peraltro complesso: in luogo del moltiplicatore 2 occorre adottare un altro numero, scelto ad hoc. Personalmente (in particolare, per le motivazioni scritte all’inizio dei questo articolo) propongo al compositore di utilizzare la scala φ-tonale, denominata 10- φtET e basata sul numero φ (cioè la sezione aurea), con una sequenza di 10 “semitoni” separati in modo equanime nei rapporti in frequenza tra loro dal numero irrazionale s, la radice decima del numero aureo:
s: 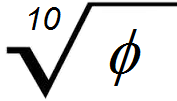 = 1,049297804…
= 1,049297804…
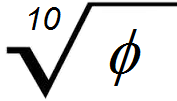 = 1,049297804…
= 1,049297804…
Ovviamente, a questo punto l’intervallo di ottava non sarà più rappresentato dal rapporto numero intero 2, ma dal rapporto φ, in una scala di dieci semitoni tale che:
s x s x s x s x s x s x s x s x s x s = φ
Dato che il valore di 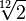 vale circa 1,05946, possiamo notare che il valore s del “semitono” della scala φ-tonale risulta essere leggermente più “piccolo” del valore S della scala cromatica occidentale 12-tET.
vale circa 1,05946, possiamo notare che il valore s del “semitono” della scala φ-tonale risulta essere leggermente più “piccolo” del valore S della scala cromatica occidentale 12-tET.
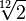 vale circa 1,05946, possiamo notare che il valore s del “semitono” della scala φ-tonale risulta essere leggermente più “piccolo” del valore S della scala cromatica occidentale 12-tET.
vale circa 1,05946, possiamo notare che il valore s del “semitono” della scala φ-tonale risulta essere leggermente più “piccolo” del valore S della scala cromatica occidentale 12-tET.
Ma l’elemento più importante e la vera novità concettuale della scala φ-tonale è che, nel suo sviluppo nelle sue note ascendenti e discendenti, si determina un andamento delle altezze di nota tale da non incrociare mai le rispettive ottave di ogni altra nota in scala. Si veda infatti nel seguito lo sviluppo delle frequenze per 4 ottave nell’intorno del La centrale 440 Hz, rispettivamente per le due scale 12tET e 10φ-tET:
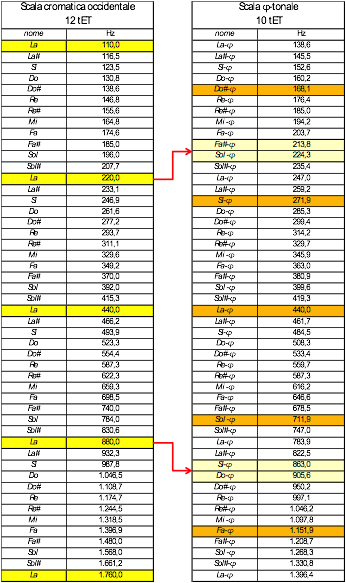
All’interno dell’ottava seguente il La centrale (La3) , la scala φ-tonale esprime circa 14 “semitoni”: il 14° “semitono” a salire (indicato Si-φ) è infatti percettibilmente più grave del La4 una ottava sopra (863,0 contro 880 Hz), mentre il 15° semitono è leggermente più acuto del La4 (905,6 Hz contro 880 Hz).
Ne consegue dunque che, nello sviluppo delle note nella scala φ-tonale, non esisterà mai alcuna coppia di “semitoni” che siano rispettivamente l’uno un’ottava inferiore o superiore dell’altro. Si tratta dunque di una sequenza di suoni assolutamente nuova, i cui rapporti “armonici” e le cui potenzialità espressive (nella sua totale mancanza di riferimento con l’intervallo di ottava) sono ancora sconosciute e tutte da esplorare.
Conclusioni
Questa in realtà non vuole (né può) essere una conclusione. Spero però possa avvenire, per il lettore musicista intrigato o almeno incuriosito dalle considerazioni teoriche esposte sopra, che esse siano un buon punto di partenza su cui riflettere e ragionare. E magari, sperabilmente, creare.
La costruzione di questa scala, grazie ai moderni strumenti elettronici di sequencing disponibili all’interno di un qualsiasi software musicale (Cubase, Sonar, ecc.) è relativamente semplice. Per quanto poi riguarda la notazione su rigo della scala φ-tonale è tranquillamente possibile continuare a utilizzare quella tradizionale su pentagramma, a partire dal La3. tenendo ovviamente presente che il significato delle note rappresenta tutt’altro che quanto siamo tradizionalmente abituati a pensare e a sentire.
Buona musica φ-tonale!
(Tabella frequenze Sistema Musicale Aureo Phi basato su LA = 432 Hz)

Audio Albums specifici:
Album dedicato alla armonizzazione delle onde cerebrali Gamma con oltre 50 minuti di musica e sonorità intonate a 432 Hertz. I brani sono progettati per indurre uno stato di energizzazione in sinergia con il riequilibrio delle frequenze Gamma per favorire l’intuizione e l’ispirazione.